un semplicissimo esperimento di fisica classica

Misurazione dell'accelerazione di gravità con il pendolo semplice

pag. 4

Prova di misurazione del modulo dell'accelerazione di gravità g mediante il pendolo semplice realizzato come dianzi descritto

Nel caso presente che illustriamo si hanno i seguenti parametri assegnati e rilevati:

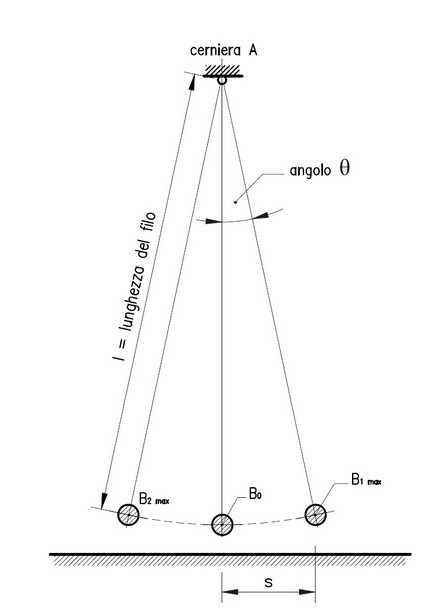
- l = lunghezza del filo = 2,684 metri ;

- s = scostamento dalla verticale assegnato = 6 cm., in questo modo per la lunghezza data si ha un angolo iniziale di oscillazione (teta, in figura) pari a circa 1°, il quale è sufficientemente piccolo in aderenza al postulato della legge del pendolo semplice, cioè con buona approssimazione;

- alla fine dei 40 cicli misurati lo scostamento orizzontale s si è ridotto a soli 3 cm. circa, cui corrisponde un angolo di oscillazione di ca. mezzo grado;

- le prime 3 misurazioni (vedi le prime 3 righe in tabella) sono riferite ad oscillazioni del pendolo contenute nel piano verticale con orientamento Est-Ovest;

- mentre la quarta misurazione riguarda oscillazioni del pendolo contenute nel piano verticale con orientamento Nord-Sud;

- come si nota non si apprezza alcuna variazione significativa del tempo totale t cronometrato al variare dell'orientamento del piano di oscillazione del pendolo, almeno con questo rudimentale sistema di misurazione; e nemmeno effettuando le misurazioni in orari diversi (per brevità non riportiamo ulteriori dati raccolti);

- la lunghezza del filo è stata controllata prima dell'inizio e dopo la fine dei quattro cicli di 40 oscillazioni susseguenti misurate;

- la prova è stata effettuata ad una altitudine di pochi metri sul livello del mare, a Roma;

- ulteriori specifiche sarebbe oziose dal momento che il nostro strumento di misura è grossolano; si ricorda che esiste tutto un campo dello scibile umano, la gravimetria, branca della geofisica, che si occupa del campo gravitazionale e delle anomalie gravitazionali;

- ecco infine i dati raccolti:

Da cui ricaviamo il valore medio del tempo totale t cronometrato complessivo per ciascuno dei 40 cicli consecutivi, e di qui il periodo T di oscillazione del pendolino (in confronto ad un ben più grande e maestoso Pendolo di Foucault, come quello esposto al Panthéon di Parigi sospeso alla sua cupola ad una altezza di 64 metri, il nostro pendolino è una pulce!) nel modo che segue :

t (media aritmetica) = 131,3425 secondi ;

T = t / n = 131,3425 / 40 = 3,28375 secondi ;  

π  =  pi greco = ca. 3,14

g = ( 4 π ² l) / T ²   =  

   = ( 4 x 3,14 ² x  2,684 ) /  3,2837 ²  =  9,81661

g = ca. 9,81 m / s ²  

Conclusioni

Come si era anticipato in premessa, la misurazione e il relativo calcolo di g mediante un siffatto pendolo è semplice ed immediata, una volta che lo si è sperimentato.

Ripetendo ulteriori misurazioni (sempre nel medesimo luogo in cui abbiamo effettuato questa prima misurazione)  il valore dell'accelerazione di gravità g locale così ricavato risultava pari appunto a circa 9,81 metri al minuto secondo quadro, coincidente con il valore approssimato di g che si utilizza comunque come dato di notevole precisione in molti campi dello scibile umano e in particolare della tecnica.

Questo valore locale qui sopra calcolato con il nostro pendolino casareccio, è naturalmente estremamente grossolano rispetto ai valori accuratissimi di g che si possono ottenere con strumenti (gravimetri) ed altre metodologie di precisione (che allo scopo utilizzano persino satelliti) possibili ai nostri giorni; per saperne di più vedi ad esempio INRiM, Istituto Nazionale di Ricerca Metrologica.

Per fare un esempio qualsiasi, per la semplice taratura delle bilance esistono delle tabelle specifiche ministeriali che convenzionalmente (perchè per quanto precisi siano i valori locali dell'accelerazione di gravità, sono sempre appunto "locali") stabiliscono qual'è il valore di g da adottare durante la taratura nei differenti comuni, località d'Italia, i quali sono ad esempio: a Roma g = 9,80352, a Bolzano g = 9,80548, a Napoli g = 9,80296, a Reggio Calabria g = 9,80063.

Sembra di avere a che fare con un'inezia, però, sapendo che il peso P di una determinata massa m varia al variare del valore dell'accelerazione di gravità  (poiché P = m x g), si può ben immaginare come per grandi quantitativi di merci ciò assuma una rilevanza significativa in relazione alla determinazione del loro peso negli scambi commerciali.